Example match-replace

Suppose we begin with this oytspace

and among the rules for the oyt labelled a is this

rule 12: ⇒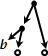

Rule 12 matches at a with the part in red

When the rd part is replaced according to the sule, the space looks like this

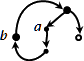
List links

A list is a sequence of oyt structures. We can think of it as each node in a 1-D space using its second link to point to an oyt at the beginning of a bunch of oyts. But. Oyt links are indistinguishable. So how to we know which link is to the next link in the list and which is to an element of the list. The trick is to use multiple oyts at each location in the list. A "list link" can be made like this, where the link is circled in blue:

The left oyt has two links, one to a 1-ary oyt and the other to a 2-ary oyt. The 1-ary oyt points to the next list link. The 2-ary oyt points to a 0-ary oyt and the list element. If the list element is a no-link oyt, both pointers from the 2-ary oyt point to 0-ary oyts. That they cannot be distinguished is not a problem because both are the same.

It is convenient to diagram a list link in fat blue arrows. The diagram above would then look like

A three element  list would be

Integer addition

Suppose integers are represented in unary. A sum task can be an oyt-list with two 1D oyt strings for the two operands.

 xxxxx move from the bottom of one list to the bottom of the other.

The result is the same oyt-list but with only one string of oyts.

Division by a constant

Division by two in unary arithmetic means cutting the number in half. This can be done in oyts as an operator that traverses a list and deletes every other element.

Representing 2-D space

triangles

Creating a 2-D space

We can create a 2-D space from triangles by starting with a rule that converts nothing into 3 triangles. No oyt-link arrows are shown; proper linking is left as an exercise. You may need multiple oyts to represent each node in this space.

rule 0

¤

⇒

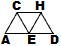
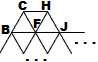
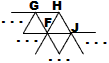
The letters denote kinds o intersections. A has edges only to the right and northeast. There is only one A intersection. H has edges left, southwest, and southeast. And so on.

Rule 1 extends the bottom row to the right continuously by adding four edges and making two new triangles:

rule 1

⇒

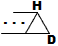
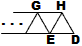
Rule 2 extends upward along the left edge. Note that the graph replacement adds the same three-triangle unit as is added by rule zero.

rule 2

⇒

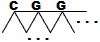
Finally, the last rule, 3, extends to the right wherever a row is above a longer row. It adds three edges to make two new triangles.

rule 3

⇒

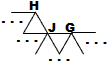
This diagram depicts where the growth is

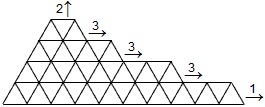
After a while we have the still growing space. (Exercise: what is wrong with this picture? Why will it not be a state of the oyt space?)

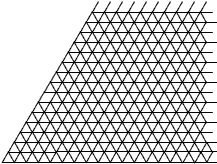
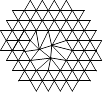
Warped space

One of the remarkable features of relativity is that space-time is warped. Oyts may or may not represent time, but they can depict warped space. Thinking of space as a collection of little points, connected like triangles.

A warp in this space means thee are more or fewer triangles at some points:

More than two dimensions

It is left as an exercise to the reader to develop a 3-dimensional space from oyts. Hint: there are various ways of filling space with tetrahedra.

Simulating a field

A "field" in physics is defined at every point in space; it has a direction and a strength at each point. Do you remember when your eacher sprinkled iron filings on a sheet above a magnet? The filings lined up with the directions of the magnetic field. The stronger the field, the more filings gathered at each point. In fact, everywhere in space has a magnetic field, stronger on some places, weaker in others. The impact on that field by the earth is why compasses work and why space-travelling particles do not fry our brains.

To repreent a field in oyts, let every point in a space have a pointer to a field element. This element will then be three numbers giving the strength of the field in three "orthogonal" directions.

Simulating photons

A photon is said to be a particle of light. Photons stream from the sun, bringing energy to the earth. It turns out that photons can also be thought of as disturbances in the electrical and magnetic fields. A moving maget generates electricity and moving electricity generates magnetism. So a photon wiggles back and forth between the electric and magnetic fields as it travels. This behavior can be represented by taking the average value of surrounding values of one field and adjusting the opposite field. And averages are simply addition folloed by division by an integer constant.