Some time ago, I became intrigued by the fact that physicists are exploring ever smaller "elementary" particles: molecules, atoms, nucleons, quarks, and now "strings." Where, I wondered, could it all end? I wondered if we could start from the "simplest" object and asked myself:

After a while I came up with an answer: oyts. These web pages explore that answer.

Oyts

An oyt is a shell holding zero, one, or two pointers to oyts. We can think of them as having little arrows; but really, you cannot "see" an oyt.

0-oyt 1-oyt   2-oyt  

Of course there could be 3-oyts, 4-oyts, and so on, but the extra complexity is not needed. Where a diagram below appears to have 3- 4- or more oyts, the junction is to be thought of as composed from some combination of 2-oyts.

Oyt spaces

Oyts and pointers do not occupy space. The size and shape of drawsings are meaningless. The above space could jsut aw well be drawn as

We could imagine all the oyts being in exactly the same "place." All that matters is the connections between them. Or we could number all the oyts and say an oyt is just the numbers of the oyts it points to. Pointers are one-way. No oyt can "know" how many other oyts link to it. Can an oyt space can have two or more disconnected collections? The two answers lead to different notions of "universe". If the oyt space is emulating our observable universe, we have no way of knowing what happens to disconnected oyts; the answer is moot.

An oyt space evolves under the direction of graph rewriting systems (GRS). Such a system is a set of rules, P→R, each comprising a pattern P that, when found in the oyt space, is to be replaced with subgraph R. The simplest case is a two-rule GRS to generate a string of oyts from nothing. (We write nothing as ¤). The first rule generates a 0-oyt from nothing. The second rule converts a 0-oyt to a 1-oyt pointing to a 0-oyt.

rule 0: ¤ ⇒

rule 1: ⇒

After applying rule 0 once and rule 1 four times, we get

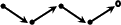
Conceptually, each oyt is the subject of its own GRS; although for many of them that GRS has no rules. These sets are a part of the description of a replacement graph, a member of R. When the replacement is inserted in an oytspace the GRS for each inserted oyt is started. It continues searching until the contents of its oyt are replaced. It is unknowable whether it continues to operate after the oyt is disconnected from the space.

Simplicity Rules

Several design decisions are intended to make oyts as primitive as possible:

• the only distinctinguishing feature of an oyt is its number of pointers. There is no way to distinguish between an oyt that points to itself and an infinitely long chain of oyts, each pointing to the next.
• Moreover, the pointers from a 2-oyt cannot be distinuished. This restriction is not rally a limitation as we will see in the "list link" example.

For true simplicity, an oyt would be an immutable entity. But that would obviate the possibility of GRS processing; the only way to generate an oytspace with some part replaced would be to generate a new oyt space. This seems a profligate way to design a universe. (Although the "many worlds" hypotheisis operates on the principle.) Some simplicity is attained by requiring that

• both pointers in a 2-oyt must be replaced at the same time.

The general task of determining if P matches somewhere in an oytspace is, at best, mathematically difficult. So simplifications are needed:

• no GRS is associated with the entire oyt space. Instead, when an oyt is created its own personal set of GRS rules is assigned to watch for patterns that begin from it. That oyt is called the target of those GRS rules and all patterns in the GRS are rooted at that target. 
• oyts in patterns can be pointed to by no more than one pointer. (This means a pattern is an acyclic directed graph, or DAG.) There are no loops in the pattern. This does not mean that a loop cannot be matched, a pattern can traverse the loop as many times as it likes; but the pattern cannot demand that it be matching a loop.
• the only match test between two oyts is whether both have the same number of pointers. Note that the match process can still be lengthy--every match of 2-oyts has to be tried twice--once with each pairing of children in the pattern to children of the oyt in the space.

This completes the rules of what constitutes an oyt space. No more. Next readings:

Examples

Advantages for describing a universe